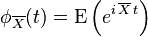观察变量分布时最重要的三个特性之一是胖-瘦(另两个是:单模-多模;对称-有偏),柯西分布和正态分布是极易混淆的分布曲线。
柯西分布也叫作柯西-洛伦兹分布,它是以与名字命名的连续,其为
其中x0是定义分布峰值位置的,γ是最大值一半处的一半宽度的。
作为概率分布,通常叫作柯西分布,也将之称为洛伦兹分布或者Breit-Wigner分布。在中的重要性很大一部分归因于它是描述受迫的的解。在中,它描述了被共振或者其它机制加宽的谱线形状。在下面的部分将使用柯西分布这个统计学术语。
x0 = 0且γ = 1的特例称为标准柯西分布,其概率密度函数为
特性
其累积分布函数为:
柯西分布的逆累积分布函数为
柯西分布的、或者都没有定义,它的与有定义都等于 x0。
取 X 表示柯西分布随机变量,柯西分布的表示为:
如果 U 与 V 是为 0、为 1 的两个独立随机变量的话,那么比值 U/V 为柯西分布。
标准柯西分布是自由度为1的特殊情况。
柯西分布是:如果 ,则
,则 。
。
如果 X1, …, Xn 是分别符合柯西分布的随机变量,那么(X1 + … + Xn)/n 有同样的柯西分布。为了证明这一点,我们来计算采样平均的:
其中, 是采样平均值。这个例子表明不能舍弃中的有限变量假设。
是采样平均值。这个例子表明不能舍弃中的有限变量假设。
洛仑兹线性分布更适合于那种比较扁、宽的曲线 高斯线性分布则适合较高、较窄的曲线 当然,如果是比较居中的情况,两者都可以。 很多情况下,采用的是两者各占一定比例的做法。如洛伦茨占60%,高斯占40%.
| 概率密度函数绿线是标准柯西分布 | |
| 累积分布函数与上图中的颜色对应 | |
| 参数 |  () () (实数) (实数) |
|---|---|
 | |
![柯西分布——正态分布的兄弟 \frac{1}{\pi\gamma\,\left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} \!](http://upload.wikimedia.org/math/1/1/0/110abf1f3bbdd637b6ddd41296caa067.png) | |
 | |
| { { {notation}}} | |
| (没有定义) | |
 | |
 | |
| (没有定义) | |
| (没有定义) | |
| (没有定义) | |
 | |
| (没有定义) | |
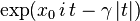 | |
外部链接
-
- , at
![柯西分布——正态分布的兄弟 f(x; x_0,\gamma) = \frac{1}{\pi\gamma \left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]} \!](http://upload.wikimedia.org/math/9/9/3/99356e5bb7fb2597cb8c0c1f6436d764.png)
![柯西分布——正态分布的兄弟 = { 1 \over \pi } \left[ { \gamma \over (x - x_0)^2 + \gamma^2 } \right] \!](http://upload.wikimedia.org/math/8/9/7/897155389ea99bdf6d8e53432ff9a9fd.png)